• 算术动力学利用数论中的对象（如椭圆曲线）和动态系统中的对象（如朱利亚集合）之间的相似性，对这两者产生新的见解。

数学家约翰·米尔诺研究课题是一个叫做复杂动力学的领域，而布朗大学的数学家西尔弗曼对这个领域知之甚少。但是，当西尔弗曼了解了一些复杂动力学的基本概念后，他发现，这与数论领域具有惊人的相似性。

乍一看，这两者就像是数学中不相关的分支。但西尔弗曼认识到，它们在某种特定的方面相互补充。数论寻找的是数字序列的模式，而动力系统实际上产生的是数字序列（就像在有规律的时间间隔内定义行星在空间中的位置的序列）。当数学家们寻找隐藏在这些序列中的数字理论模式时，两者就会合并。

经过几十年的研究，数学家们戏剧性地加强了数学两个分支（动力系统与数论）之间的联系，并建立了一个全新的领域，即算术动力学。

这个领域的范围还在继续扩大。在去年发表在《数学年鉴》上的一篇论文中，三位数学家将数论与动力系统的联系发展到了一个全新的高度。这样，他们解决了数论中一个存在了几十年的问题的一部分，这个问题以前似乎与动力系统没有任何明确的联系。

新的证明量化了一种曲线在周围空间中与特殊点相交的次数。数论学家以前想知道，对于交集的数量是否有上限。证明的作者利用算术动力学证明了某一特定曲线集合有一个上限值。

曲线运动

2010年5月，一群数学家聚集在巴巴多斯的一个小型研究机构讨论数学。这是算术动力学发展的关键时刻。它汇集了数论专家，比如西尔弗曼，以及动力系统专家，比如德马科和克里格。他们的目标是，通过进一步挖掘这两个领域的联系来解决更多的问题。

他们的出发点是数论的中心对象之一，椭圆曲线。就像圆和线一样，椭圆曲线既是数字又是形状。它们是一对数字（x和y），可以作为一个代数方程的解，比如 y^2 = x^3 ? 2x。这些解的图形创建了一个几何形状，看起来有点像一条垂直的线挤出了一个气泡。

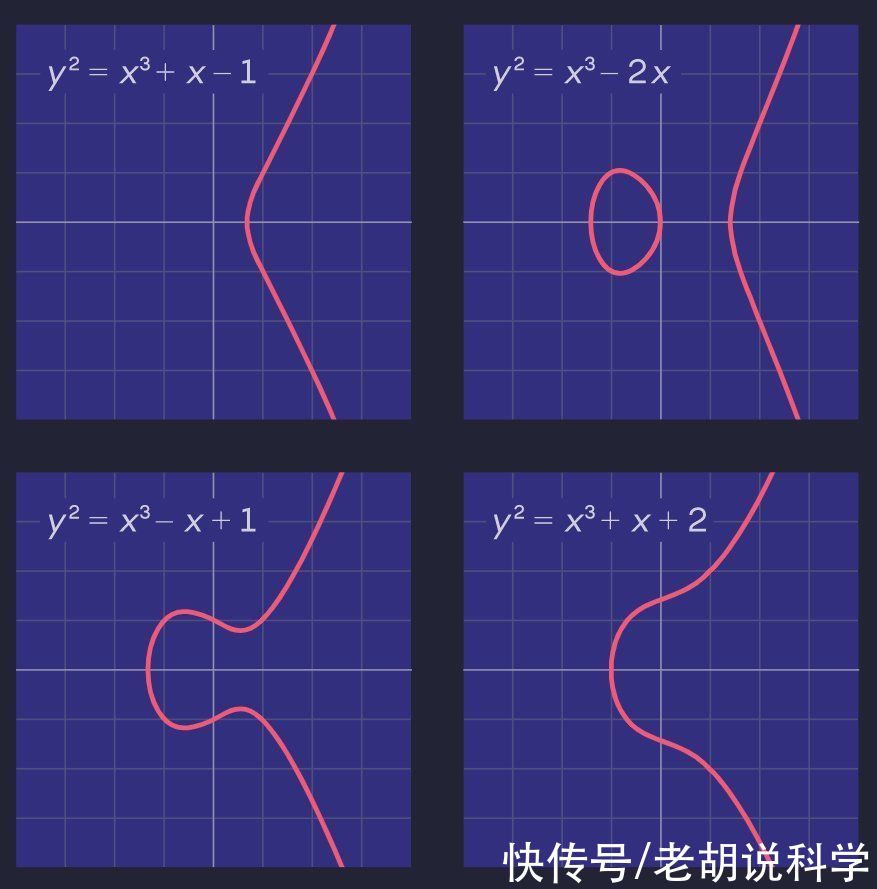
请点击输入图片描述（最多18字）

• 椭圆曲线，椭圆曲线具有丰富的结构。它们是数论研究的一个重要对象。

数学家们一直对量化和分类这些曲线的各种性质很感兴趣。到目前为止，最著名的是安德鲁·怀尔斯在1994年对费马大定理的著名证明，这是一个关于哪些方程的解是整数的问题。这个证明很大程度上依赖于对椭圆曲线的研究。一般来说，数学家们关注椭圆曲线，是因为它们即不是微不足道不值得研究，也不是难到无法研究。

佐治亚理工学院的数学家马特·贝克说：

数学家们对椭圆曲线上的点特别感兴趣，这些点在曲线上以一种特殊的方式移动。在椭圆曲线上，你可以用标准加法将点彼此相加，但这种方法不是很有用，因为和不太可能是曲线上的另一个点。

但是椭圆曲线有一个特殊的内部结构，它创造了一种不同类型的算术。这种结构称为群，使用其自包含的算术规则将点相加的结果是完全不同的。如果你根据群结构在椭圆曲线上加两点，和总是曲线上的第三点。如果你无限次重复这个过程，结果就是无限多的点都在椭圆曲线上。（关于群论的更多细节，可以阅读这篇文章：由浅入深，轻松理解抽象代数的重要分支——群论 ）

不同的起点会产生不同的序列。“大本营点（home base）”是具有非常独特属性的起点。如果你反复地把这些点相加，它不会产生无限的新点序列。相反，它创建了一个循环，最终回到开始时的点。

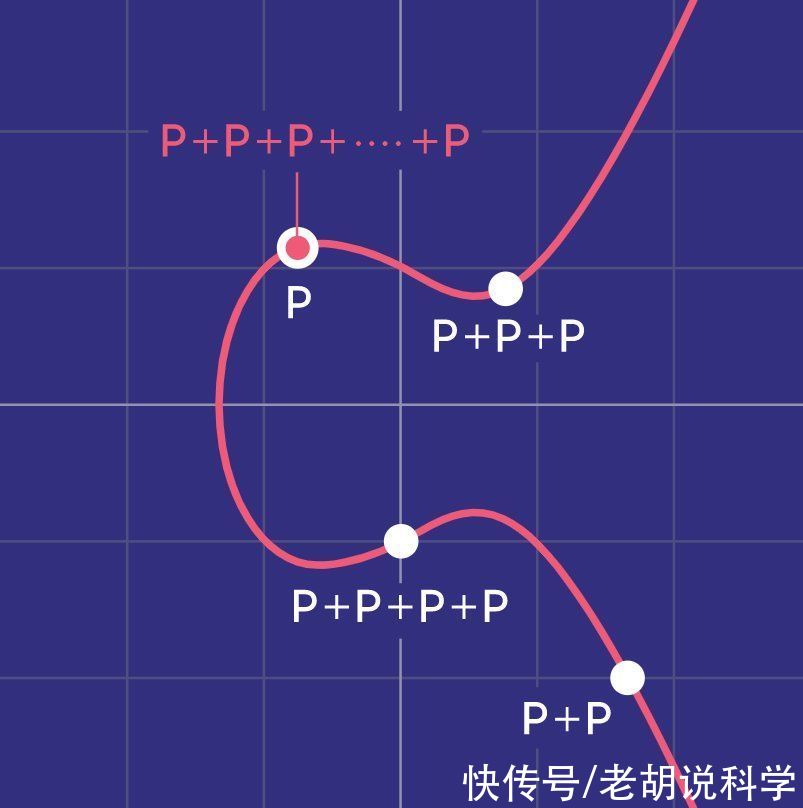
请点击输入图片描述（最多18字）

• 扭转点，当一个扭转点被反复加到自身上时，结果最终会回到起始点。

这些产生循环的特殊起始点称为扭转点。他们是数字理论家们最感兴趣的。它们也与动力系统的某一特定类型的点有惊人的对应关系，正是这种对应关系真正让算术动力学成为可能。

重复模式

动力系统经常被用来描述现实世界的现象，根据一个重复的规则向前移动，就像一个球根据牛顿定律的反弹。将一个初始值插入到一个函数中，然后得到一个输出，这个输出将成为新的输入。

一些最有趣的动力系统是由像 f(x) = x^2 ? 1